量子レイトレーシングに思いを馳せる
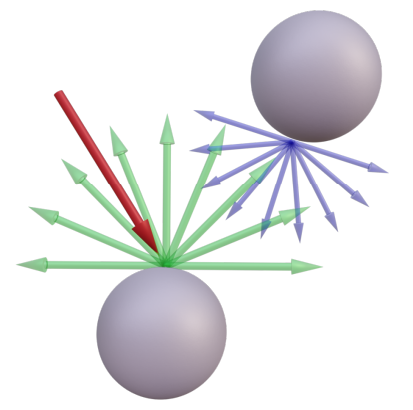

右: Towards Quantum Ray Tracing [Luís, 2022]
この記事は レイトレ合宿8 アドベントカレンダー 4週目の記事です。
1980年代から概念が提唱されるも未だに「なんだかよくわからないけど凄そうワード」として君臨し続けている量子コンピューターですが、 最近突如 arXiv に量子コンピューターを用いたレイトレーシングの論文が 2件公開されていました。
我々の知らない間にいつの間にか量子レイトレーシングは実用化されていたのでしょうか。 ひょっとすると、ニュースでよく見かけるように超並列計算で無数にレイを飛ばすことでスパコンだと数万年かかるシーンについて数秒でレンダリングできてしまうのでしょうか。 (参考:量子コンピュータ 9000兆倍の破壊力 | 日経クロステック(xTECH))
もしそうだとしたらサンプリングの改善とかで地道にノイズを減らしたりしている場合ではありません。 流行に乗り遅れない為にも、今回は上記の論文を通して最新の量子レイトレーシングの概要を追いかけていきます。
続きを読むレイトレ的観点でみる2Dイラストテクニック
この記事はレイトレアドベントカレンダー2020の記事です。 qiita.com
レイトレと言いつつほぼ物理ベースシェーディングの記事であって特にレイは飛ばしていませんが、 物理ベースシェーディングはレイトレなのでこの記事もレイトレです。 レイトレってなに?
前置き
人や物、風景などを描いた2Dイラストは、スタイライズド表現の程度に差はあれど基本的には現実の物体や現象をベースとしています。 そのため、"よい表現"をするには現実の事象に対する"よい観察"が必要となりますが、 その"よい観察"のためには事象の裏側にある"仕組み"を知っておくことがしばしば有効です。 例えば、人を描くならば美術解剖学を学んでおくとよいし、風景などを描くならばパースの知識があったほうがよいとされます。 しかし何故か、2Dイラストにおける物体のシェーディング・ライティング(色塗り)の文脈において3DCG向けの物理ベースレンダリングやレイトレーシングが引き合いに出されることはあまり多くありません。
そこで本記事では、2Dのイラストの制作において経験的に知られている種々のテクニックについて、 物理ベースレンダリングやレイトレの観点から何らかの意味付けを与えるような考察を行っていきます。 ある種の思考実験であって何かしらの一般的結論や方法論を与えるような試みではありませんが、 3DCGの知見を2Dイラストに活かしたり、またその逆を行ったりするような、 何らかの面白い表現のヒントになればと思います。
なお、 神絵師でもなければ Wenzel Jakob でもない私が経験則的なイラストテクニックに対し想像で理屈を付けていくという企画の趣旨上、 実は事象の一部の説明にしかなっていなかったり、また全く違うことを言っているという可能性もあるという点はご了承ください。 (識者の意見は Twitter とかで受け付けています。)
続きを読むAccurate Appearance Preserving Prefiltering for Rendering Displacement-Mapped Surfaces [Wu 2019]

SIGGRAPH 2019 の論文。読んだのでメモ。
ディスプレースメントマップをダウンサンプリングして低解像度化した場合、 その低解像度テクスチャを適用したジオメトリは 元の高解像度テクスチャを適用した場合に比べて表面の明示的な凹凸が減る。 その結果、 シャドーイング・マスキング効果やそれに付随する局所散乱の効果が変化してしまい レンダリング時の見た目が変わってしまうという問題が引き起こされる。
この論文では、 低解像度ディスプレースメントマップを使いつつ元の見た目を再現するため、 シャドーイング・マスキング効果と局所散乱の変化を補償するようなスケーリング関数を提案し、 またそれを事前計算する方法とその効率的なエンコーディングについて述べている。
なお、この論文を読んで再現実装をしてみたものを自分の github リポジトリ上にアップしている。
続きを読むLuminance-Contrast-Aware Foveated Rendering [Tursun 2019]
https://www.pdf.inf.usi.ch/projects/AdaptiveFoveation/

SIGGRAPH 2019 の論文。
フォービエイテッドレンダリングは、ユーザが注視している点でのレンダリングは精細に、逆に周辺視野では荒く行うことでレンダリングの高速化をする技術である。 近年、ディスプレイなどの表示側デバイスがどんどん高解像度化・高フレームレート化しているのに対し描画側のデバイスの性能向上が追いついていない問題への有効な対処法として、 VR 関連の文脈でも注目されることが多い。
既存の手法では、注視点からどれだけ離れているか (eccentricity: 偏心角) のみに応じて描画解像度を変化させていたが、 この論文では、描画される画像の知覚上でのコントラストと、知覚可能になるしきい値をモデル化し、それを元に描画解像度を決定することで より効率的でアダプティブなレンダリングができるとしている。
続きを読む格闘ゲーム AI 論文 11 本斜め読み
現在自分が作っている横スクロールアクションについて 少し凝った AI を搭載したいと考えているので、システムとしては近そうな格闘ゲームの AI についての論文を漁った。
Fighting Game AI Competition という格闘ゲーム AI のコンペティションに関連する論文が多い。
以下なんとなくジャンルに分けつつ概要を載せる。 気が向いたら個々のトピックの記事とかも書きたい。
続きを読むA Radiative Transfer Framework for Spatially-Correlated Materials [Jarabo 2018]
[1805.02651] A Radiative Transfer Framework for Spatially-Correlated Materials

SIGGRAPH 2018 の論文。
ボリュームレンダリングに使用する放射輸送方程式 (RTE) は媒質内の粒子が空間的に相関性のない配置をしていることを前提としていたが、 実はこの粒子の空間的な相関というのはボリュームの見た目に大きな影響を及ぼす。 この論文では、 粒子間の空間的相関性を考慮した RTE は Generalized Boltzmann Equation (GBE) として他分野で提案されていたものを レンダリングのフレームワーク上で適用できるように拡張し、 粒子間の空間的相関性を考慮したボリュームレンダリングを可能にすることを目的としている。
続きを読む