Accurate Appearance Preserving Prefiltering for Rendering Displacement-Mapped Surfaces [Wu 2019]

SIGGRAPH 2019 の論文。読んだのでメモ。
ディスプレースメントマップをダウンサンプリングして低解像度化した場合、 その低解像度テクスチャを適用したジオメトリは 元の高解像度テクスチャを適用した場合に比べて表面の明示的な凹凸が減る。 その結果、 シャドーイング・マスキング効果やそれに付随する局所散乱の効果が変化してしまい レンダリング時の見た目が変わってしまうという問題が引き起こされる。
この論文では、 低解像度ディスプレースメントマップを使いつつ元の見た目を再現するため、 シャドーイング・マスキング効果と局所散乱の変化を補償するようなスケーリング関数を提案し、 またそれを事前計算する方法とその効率的なエンコーディングについて述べている。
なお、この論文を読んで再現実装をしてみたものを自分の github リポジトリ上にアップしている。
提案手法の概要
低解像度ジオメトリに適用するシェーディングモデルとして、
まず、シャドーイング・マスキング効果の減少については考慮しないシンプルなモデル を考える。
ダウンサンプリング後の各テクセルに対応するテクスチャ座標系領域をパッチと呼ぶこととすると、
は
ベースとなる BRDF
に対して
あらかじめ高解像度テクスチャから計算した各パッチ内での法線分布 (NDF) を畳み込むことで得られる。
このとき、NDF はテクスチャ座標系上で空間的に変化するため特に SVNDF (Spatially Varying NDF) と呼ばれ、
同様に BRDF
は SVBRDF (Spatially Varying BRDF) と呼ばれる。
この SVBRDF は 先述したように (高解像度ジオメトリでは起こるはずだった) 微細な構造によるシャドーイング・マスキング効果を無視しており、 また当然それに付随する微細構造内の局所散乱についても考慮していない。
そこで提案手法では、
最終的に低解像度ジオメトリに適用する SVBRDF を としたとき、
\begin{align} f_{low}(x, \omega_i, \omega_o) = R(x,\omega_i,\omega_o) f'_{low}(x,\omega_i,\omega_o) \end{align}
となるようなスケーリング関数 を用いてシャドーイング・マスキング効果と局所散乱を補償する。
ディスプレースメントマップのダウンサンプリング
提案手法の詳細に行く前に、まずディスプレースメントマッピングのダウンサンプリングをどうやって行うかについて述べる。
ダウンサンプリングは以下のロス関数を最小化するような低解像度テクスチャ を求める作業として行われている。
\begin{align} \displaystyle L(h_{low}) = \sum _u \sum_v \left|\left| \tilde{s}_{uv} - \tilde{s}^{*}_{uv} \right|\right|^2 + w\left|\left| \Delta h_{low}(\frac{u}{2^{l'}}, \frac{v}{2^{l'}}) \right|\right|^2 \end{align}
細かい説明は省くが、基本的にはこのロス関数は各パッチにおける平均の傾きが高解像度テクスチャと低解像度テクスチャで一致するようにしているだけである。
少し特殊なのはラプラシアンの二乗として正規化項を加えていることで、これには高さの凸凹を抑える効果がある。 おそらく、テクスチャによっては変にピーキーな傾きのテクセルが出てしまう場合があって、それをこの正規化項で抑えたいのだと思われる。 (ラプラシアンは傾きの発散なので、山や谷になっている部分で絶対値が大きくなる。)
また、SVNDF についてもこのタイミングで計算を行っておく必要がある。 論文中では von Mises-Fisher 分布を使って各パッチに対応する NDF を近似してエンコードしていた。
スケーリング関数を求める
実効 BRDF
以下の項ではスケーリング関数を実際に式として求めていくが、 そのために必要な実効 BRDF (effective BRDF) の概念について先に触れておく。
実効 BRDF は、
微細な構造を持つジオメトリ 対してある BRDF
を適用した場合に、
ある微小領域
内のジオメトリ
が視線方向
に対して平均してどのような反射を行うのかを表す。
(やや乱暴だが) 直感的に言うと、実効 BRDF は
を
方向から見た場合に
見えている部分が反射している輝度の平均を表現でき、
を遠くから見た場合の見た目を近似するために使用される。
以下では、
ジオメトリ に BRDF
を適用して
領域
を視線方向
から見た際の実効 BRDF について、
特に単一散乱パスだけを考えたものを
、
複数散乱成分まで考慮したものを
として表す。
なお、特殊な場合を除き
や
の値を求めるには
上での明示的なパストレーシングを行う必要がある。
またこのとき、
は
パスの始点は常に
内の点であるが、
パス全体が
内に収まるわけではないことに注意。
単一散乱のみを考慮したスケーリング関数
先述したように、スケーリング関数 は
\begin{align} f_{low}(x, \omega_i, \omega_o) = R(x,\omega_i,\omega_o) f'_{low}(x,\omega_i,\omega_o) \end{align}
という形式で SVBRDF をその名の通りスケーリングするために使用される。
ここでまず、簡単のため、高解像度ジオメトリにおいてパッチ内で単一散乱して出ていくパスのみを考慮した場合のスケーリング関数の定義を考える。
スケーリング関数の最終的な目的は、
を適用した低解像度ジオメトリに対し、
元の BRDF
を適用した高解像度ジオメトリと同様の見た目をもたせることである。
さらに正確に言うと、
を含むパッチ
内の低解像度ジオメトリを
、高解像度ジオメトリを
としたときに、
任意の
の組について
\begin{align} f^{eff}(\omega_i,\omega_o; \cal{G}_{low}(\cal{P}_x), f_{low}) = f^{eff}(\omega_i,\omega_o; \cal{G}_{orig}(\cal{P}_x), f_{orig}) \tag{*} \end{align}
を成り立たせることがスケーリング関数の目的である。
ここで注目するのが、単一散乱パスのみを考えた場合、 実効 BRDF は入力する BRDF について線形となることである。 つまり、
\begin{align} f^{eff}(\omega_i,\omega_o; \cal{G}_{low}(\cal{P}_x), f_{low}) &= f^{eff}(\omega_i,\omega_o; \cal{G}_{low}(\cal{P}_x), R(x,\omega_i,\omega_o) f'_{low}) \\ &= R(x,\omega_i,\omega_o) f^{eff}(\omega_i,\omega_o; \cal{G}_{low}(\cal{P}_x), f'_{low}) \end{align}
となり、これを上式 (*) に代入すると
\begin{align} \displaystyle R(x,\omega_i,\omega_o) = \frac{f^{eff}(\omega_i,\omega_o; \cal{G}_{orig}(\cal{P}_x), f_{orig})}{f^{eff}(\omega_i,\omega_o; \cal{G}_{low}(\cal{P}_x), f'_{low})} \end{align}
が得られる。
複数散乱を含めたスケーリング関数
同様に、パッチ内での複数散乱を含めた場合について考える。
複数散乱を含めた場合のスケーリング関数を特に と表記すると、
この
は、複数散乱の実効 BRDF について
\begin{align} f^{eff}_{ir}(\omega_i,\omega_o; \cal{G}_{low}(\cal{P}_x), f_{low}) = f^{eff}_{ir}(\omega_i,\omega_o; \cal{G}_{orig}(\cal{P}_x), f_{orig}) \end{align}
を成り立たせる必要がある。
ここで問題になるのが、 は
について線形でないことである。
そのためこのままだと単一散乱のように
を求めることはできない。
上式のまま求めることも理論上可能であるが、かなり計算コストが重く現実的ではない。
そこで、ひとつ仮定を置く。 ジオメトリ上での距離の "遠い" 反射の計算については、 本来は高解像度ジオメトリと低解像度ジオメトリとでは微妙に差異があるが、 これが低解像度ジオメトリ上での明示的なパストレーシングで十分に近似されるとする。
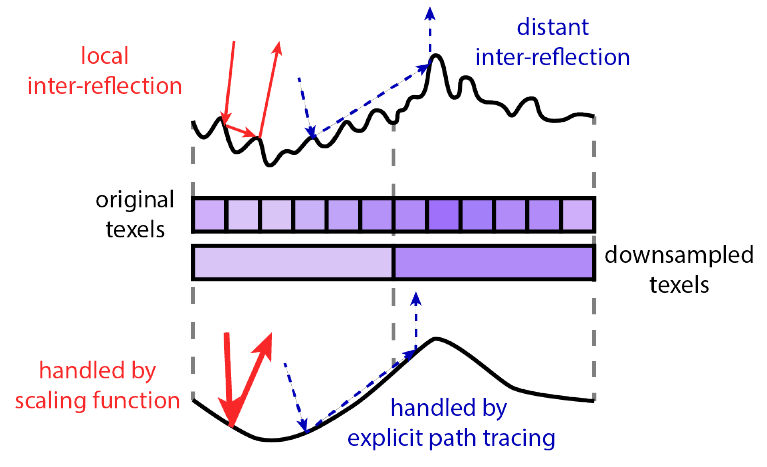
(図においてジオメトリが各テクセル中央に位置する頂点同士を繋いだ直線群で構成されていないが、 高さを単に線形補間するのではなくもっと一般化した感じで描かれている?)
ここで言う "遠い" 反射というのがやや分かりづらいが、 ディスプレースメントマップのダウンサンプリングで消失するディティール以内での反射が "局所的な" 反射であり、 それ以上の距離で起こるのが "遠い" 反射である。
この仮定によって、 スケーリング関数や実効 BRDF は "局所的な" 反射についてのみ責任をもつこととなり、 低解像度ジオメトリの実効 BRDF は常に単一散乱成分のみを考えればよくなる。 これにより結局、 \begin{align} f^{eff}_{ir}(\omega_i,\omega_o; \cal{G}_{low}(\cal{P}_x), f_{low}) = f^{eff}(\omega_i,\omega_o; \cal{G}_{low}(\cal{P}_x), f_{low}) \end{align} となる。
以上の議論から、最終的に
\begin{align} \displaystyle R_{ir}(x,\omega_i,\omega_o) = \frac{f^{eff}_{ir}(\omega_i,\omega_o; \cal{G}_{orig}(\cal{P}_x), f_{orig})}{f^{eff}(\omega_i,\omega_o; \cal{G}_{low}(\cal{P}_x), f'_{low})} \end{align}
が得られる。
スケーリング関数の因数分解
以上からスケーリング関数 を求める方法は分かったが、
実際には、
が 6 次元の高次元な関数であることから
その事前計算やメモリ上への保存には困難が生じる。
そこで、提案手法ではさらに
を
空間についての関数
(2D) と
方向についての関数
(4D) の
2 つの低次元な関数の積として近似可能であること、
またそれらが低周波な関数であるために効率的にテーブル化可能であることを示している。
ランク 1 因数分解
2 種類の異なるシーンにおいて、
計算によって をテーブル化し、
それらのテーブルをそれぞれ行列として表現したものを特異値分解にかけると、
最も大きい特異値が 95% 以上のエネルギーを持つことがわかった。
これは
が
ランク 1 因数分解可能であること示しており、
\begin{align} R_{ir}(x, \omega_i,\omega_o) \approx T_{ir}(x) S_{ir}(\omega_i, \omega_o) \end{align}
となる。
(正直あまりわかってない)
関数の滑らかさ
こちらについても同様に、
2 種類の異なるシーンにおいて
と
のテーブル化の解像度を変えつつ実験し、
それらが低解像度で表現可能であることを実験的に示している。
T, S の計算
空間についての関数 は、
位置
を固定して方向
を変化させた場合の
の平均として求められる。
逆に、方向についての関数 は、
方向
を固定して位置
を変化させた場合の
の平均となる。
(論文中の式 (24) ではテクスチャ座標
についての積分であることに注意。)
なお、 は
その値を求めたあとで平均の値が 1 となるように正規化される。
(意味を持つのは
と
の積の値だけなので、
か
のどちらか一方は正規化しておかなければ値が定められない。)
リミテーション
高解像度ジオメトリが急なエッジを持っている場合などにおいては ジオメトリ上の ”遠い” 反射の計算が低解像度ジオメトリ上の明示的なパストレーシングで近似可能という仮定が成り立たず、 その場合には複数散乱の近似の精度が低くなるらしい。 そのほか、事前計算はディスプレースメントマップとベース BRDF との組に対して行うため、 ベース BRDF を変更する場合には再計算が必要となる、 などのリミテーションが挙げられている。