Microfacet-based Normal Mapping for Robust Monte Carlo Path Tracing [Schüssler 2017]

f:id:mizuooon:20180127185756p:plain

SIGGRAPH ASIA 2017 の論文。古典的なノーマルマッピングはジオメトリの形状を変えずに法線情報のみに変更を加えるため物理的に正しくないモデルになっており、物理ベースのレイトレーシングを行った際には種々の問題を引き起こす。例えば上図のように、視線方向が法線の裏側になってしまったり反射したレイの方向がジオメトリの内部に行ってしまったりしてエネルギーロスが起きてしまうなど。この論文では以上のような問題の解決のため、マイクロファセットをベースとして古典的なバンプマッピングを置き換えるモデルを提案している。

なお、この論文を読んで再現実装をしてみたものを自分の github リポジトリ上にアップしている。

GitHub - mizuooon/Xitils

目的

ノーマルマッピングは現在もリアルタイム/非リアルタイムを問わず非常によく使われているが、 CGの歴史上古い手法であり、物理ベースでの正しさを特に意識していないモデルになっている。リアルタイムのレンダリングではちゃんとパストレとかしないのでその辺はいまだに問題になっていないが、非リアルタイムのレンダリングでは先述のような問題を招く。ディスプレースメントマッピングはジオメトリ自体を操作するために物理的に正しい結果が得られるが、描画コストはノーマルマッピングに比べかなり高くなり、そのままノーマルマッピングを代替できるとは言い難い。この論文で提案するモデルは、ノーマルマッピングのように控えめコストで、同じような効果が得られ、なおかつ物理的にも正しいことを目標としている。

ノーマルマッピングの問題点

ノーマルマッピングの問題点を具体的に述べると以下になる。

非相反性

ジオメトリの法線を $\omega_g$ 、ノーマルマッピングで置き換えられたシェーディング用法線を $\omega_s$ 、視線方向を $\omega_i$ 、反射方向を $\omega_o$ とする (下図参照)。

f:id:mizuooon:20180127200323p:plain:w350

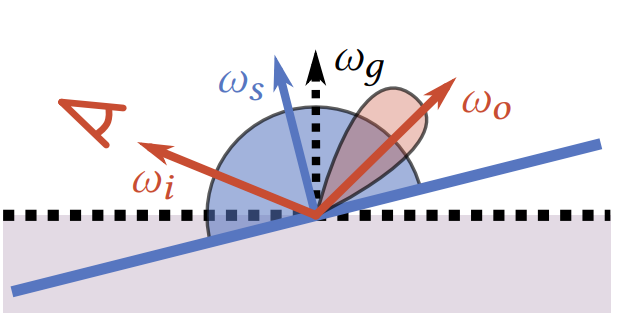
このとき、ノーマルマッピングを適用したBRDFを $\overline{f}$ とすると、 $\overline{f}$ は $\omega_s$ を法線とする BRDF $f_{\omega_s}$ を使い以下のように表される。

$\displaystyle \overline{f}(\omega_i,\omega_o) = f_{\omega_s}(\omega_i,\omega_o) \frac{ \langle\omega_o, \omega_s\rangle }{ \langle\omega_o, \omega_g\rangle }$

要するに BRDF にコサイン項 $\langle\omega_o, \omega_g\rangle$ を掛けた際にそれを $\langle\omega_o, \omega_s\rangle$ にすげ替えてやろうということである。だがこれは係数部分せいで $\omega_i, \omega_o$ についての対称性を失っており、 BRDF の満たすべき条件のひとつであるヘルムホルツの相反性を満たしていないことになる。

このことはバイディレクショナルパストレーシングでライトパスを構成する際に問題となる。インポータンスサンプリングを行う際、上記のアイパス用に考えた BRDF は非相反性によりそのまま使用することができないため、通常は $f_{\omega_s}(\omega_i,\omega_o) \langle\omega_i, \omega_g\rangle$ に比例した PDF でサンプリングを行うしかない。しかし、この場合における上記の BRDF の寄与を $f_{\omega_s}(\omega_i,\omega_o) \langle\omega_i, \omega_g\rangle$ に比例する形にして書き直すと以下のようになる。

$\displaystyle \overline{f}(\omega_i,\omega_o)\langle\omega_i, \omega_g\rangle = f_{\omega_s}(\omega_i,\omega_o) \langle\omega_i, \omega_s\rangle \frac{ \langle\omega_o, \omega_s\rangle \langle\omega_i, \omega_g\rangle }{ \langle\omega_o, \omega_g\rangle \langle\omega_i, \omega_s\rangle }$

これは $\omega_o$ か $\omega_i$ が $\omega_s$ に対して垂直に近い場合には無限に近い値を取る。このような場合には正常なインポータンスサンプリングができず、非常に大きい分散を持った結果しか得られなくなる。

BRDF の定義域

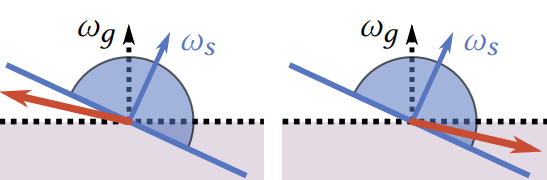
これは冒頭でも少し触れた問題である。 $\omega_g$ に対応する半球と $\omega_s$ に対応する半球は異なっていて、 BRDF $\overline{f}$ の定義域はこの半球同士が重なった狭い領域となる。このとき、未定義域の寄与はゼロとするとエネルギーロスが起きることになる。また特に、視線方向が下図左のように $f_{\omega_s}$ の定義域から外れる場合があり、このような領域は黒い縁として描画されることになる。さらに、材質がスペキュラのときは反射したレイの方向がジオメトリの内部になる場合(下図右)にも黒い縁が現れる。

f:id:mizuooon:20180127223500p:plain

エネルギー保存則違反

エネルギー保存則を満たすには、以下の式が両方満たされている必要がある。

$\displaystyle 1 \geq \int_{\Omega} \overline{f}(\omega_i,\omega_o)\langle\omega_o,\omega_g\rangle d\omega_o$

$\displaystyle 1 \geq \int_{\Omega} \overline{f}(\omega_i,\omega_o)\langle\omega_i,\omega_g\rangle d\omega_i$

ここで、 $\overline{f}$ の非相反性により $\displaystyle \int_{\Omega} \overline{f}(\omega_i,\omega_o)\langle\omega_o,\omega_g\rangle d\omega_o \neq \int_{\Omega} \overline{f}(\omega_i,\omega_o)\langle\omega_i,\omega_g\rangle d\omega_i$ であることに注意。

このとき、ふたつめの式は以下のようになる。

$\displaystyle 1 \geq \int_{\Omega} \overline{f}(\omega_i,\omega_o)\langle\omega_i,\omega_g\rangle d\omega_i = \frac{\langle\omega_o, \omega_s\rangle}{\langle\omega_o, \omega_g\rangle} \int_{\Omega} f_{\omega_s}(\omega_i,\omega_o)\langle\omega_i,\omega_g\rangle d\omega_i$

この式は $\omega_o$ が　 $\omega_g$ に対し垂直に近い場合に満たされなくなり、結果エネルギー保存則が成り立たなくなる。

よく取られる対策

上記のような問題のうち、見た目上で特に気になるのは黒い縁が見えるという問題である。これは BRDF の未定義域にレイがはみ出た場合に起きる問題なので、 BRDF の定義域を無理やり広げてやるという対策が実用上は採用されてきた。これは具体的には、レイの方向が BRDF の未定義域にはみ出た場合に、シェーディング法線の方向を曲げてやる、もしくは全く別の BRDF に置き換えてやる、という方法である。こうした方法は黒い縁の問題を解決するものの、非相反性やエネルギー保存則違反の問題についてはより悪化させることとなる。

提案手法

この論文では、マイクロファセットモデルをベースとしたモデルで法線の操作を行うことを提案している。マイクロファセットモデルはレイとジオメトリの交差判定に影響を与えないほど小さい凸凹がジオメトリの表面に存在することを想定したモデルであり、完全な平面上で法線を操作するノーマルマッピングと比較して幾何学的に有効な条件下での議論が可能なので物理的に正しいモデルが導けることが期待できる。

マイクロサーフェス

微小な凸凹を表すマイクロサーフェスの形状は以下のようなものを考える。 $\omega_p$ はノーマルマッピングにおける $\omega_s$ に相当し、シェーディング法線を向けたい方向を表す。また $\omega_t$ はマクロなジオメトリ平面についての接線方向を指しているベクトルである。

f:id:mizuooon:20180128024626p:plain:w350

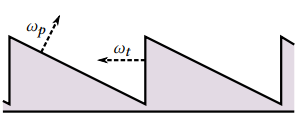
半分の視点から $\omega_t$ の面が見えるのが気にはなるが、まあ直感的にも妥当な感じがする。

マイクロファセットの関数

これをマイクロファセットモデルとして扱うには法線分布関数 (NDF) や幾何減衰項を定義する必要がある。

先述のマイクロサーフェスについて、NDF は以下のように定義できる。

$\displaystyle D(\omega_m) = \frac{\delta_{\omega_p}(\omega_m)}{\langle\omega_p,\omega_g\rangle} + \frac{\delta_{\omega_t}(\omega_m) \sqrt{1-\langle\omega_p,\omega_g\rangle^2} }{\langle\omega_p,\omega_g\rangle}$

上式ひとつ目の $\omega_p$ についての項の係数は NDF の満たすべき以下の条件から定まる。

$\displaystyle \int_{\Omega} D(\omega_m) \langle\omega_m,\omega_g\rangle d\omega_m = 1$

さらに、ふたつ目の $\omega_t$ についての項の係数はマイクロサーフェスの二種類の面の面積比から求められる。

幾何減衰項 $G$ については、入射光についての遮蔽確率と反射光についての遮蔽確率に相関が無いと仮定すると、以下のようにふたつの $G_1$ の積からなる $G_2$ として定義できる。

$\displaystyle G_2(\omega_i,\omega_o,\omega_m) = G_1(\omega_i,\omega_m)G_1(\omega_o,\omega_m)$

$G_1(\omega_i,\omega_m)$ は $\omega_i$ 方向から入射した光が $\omega_m$ を向いている面と交差する前に他の面に遮蔽される確率であり、(詳細は省略するが)簡単な幾何学計算から求められる。

こうした $D$ と $G_2$ はマイクロサーフェスモデルの BRDF 定義で物体微小表面のプロフィールとして使用される。

マイクロサーフェスモデルの BRDF

マイクロサーフェスの BRDF を求める際に問題となるのが、その微小な凸凹の構造により、マイクロサーフェス上でレイの複数散乱が起きうるということである。

この複数散乱後の BRDF の値の計算と反射後のレイ方向のサンプリングは、一般には、実際にマイクロサーフェス上でのレイのランダムウォークを行うことで求められる。

垂直小平面の BRDF

$\omega_t$ を向いている垂直小平面の BRDF $f_t$ は、比較的自由に選ぶことができる。

$f_t$ が完全拡散の場合、マイクロサーフェスについて複数散乱を考慮した BRDF を解析的に求められる。

また、 $f_t$ をスペキュラとする場合も考えられ、このときは二回散乱までを考慮した BRDF ならば解析的に求められる。

ただし、解析的に BRDF を求められる場合でも、反射したレイのインポータンスサンプリングにはまたランダムウォークを行う必要があるらしい。

結果とか

黒い縁が描画されるのを防げたりでいい感じの見た目が得られ、 (複数散乱をちゃんと計算する場合)エネルギー保存則を満たし、相反性についても満たしている。

古典的なノーマルマッピングの見た目と比べた場合、 $f_t$ をスペキュラとして二回散乱までを計算するモデルが一番近い結果が得られるらしい (エネルギーのロスは生じるが)。提案手法の Mitsuba 上の実装も提供されているが、そのモデルがデフォルトとして設定されている。

パフォーマンスについてはこのデフォルトモデルの場合、 (シェーディング計算にかかる時間が極端に支配的でない場合) 10%ほどノーマルマッピングよりも重くなる程度らしい。

提案手法の問題点としては、メッシュを描画する際には頂点間で法線を補間して面を描画することが一般的であるが、このような場合にはジオメトリ形状と法線情報が完全には一致していないために計算がおかしくなり、少しエネルギーのロスが起きるということが挙げられる。 (それでもなおノーマルマッピングと比較してロスは抑えられている)

水鳥コンビナート

CGとか